Measuring the Quality of Generated Images

In this blog post, we will look at two different methods that can be used to evaluate the quality of generated images.

Inception Score

The Inception Score was proposed by Salimans et al. in 2016. The score evaluates generated images with respect to two characteristics:

• Classifiablility: Do the images contain recognizable content?
• Diversity: Do the images sufficiently differ from each other?

Before we look at these characteristics, we first have to introduce an important concept from the field of information theory called entropy, pioneered by Claude Shannon.
The entropy of a probability distribution is the expected amount of information contained in an event drawn from that distribution. When we say that an event contains much information, we mean that the event is very surprising.
Consider the following probability distribution:

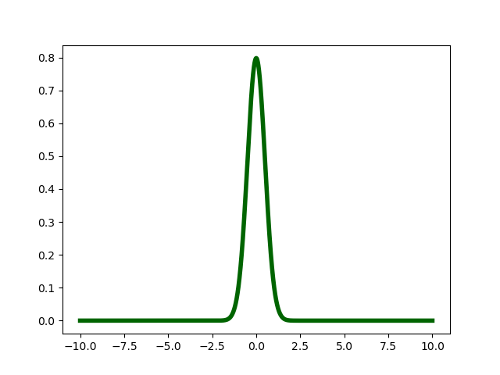
This is a Gaussian distribution with mean 0 and standard deviation 0.5. The values that we can draw from this distribution can possibly range from minus infinity to plus infinity. However, if we drew some samples from this distribution, most of them (> 99%) will lie in the range [-1.5, 1.5]. This means that for most of the samples we draw, the result would not be surprising because we can predict the outcome with high certainty. In other words, this distribution has low entropy.

Now consider in contrast this probability distribution:

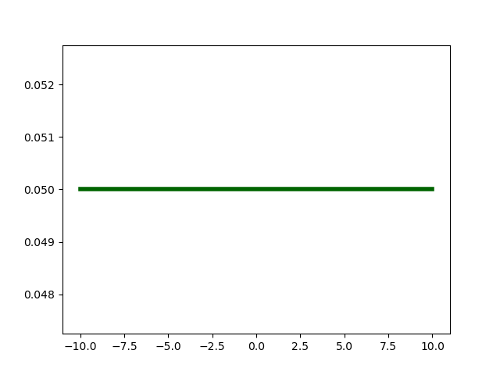
This is a Uniform distribution over the interval [-10, 10]. Any value we draw from this distribution will lie in the range of [-10, 10]. However, for this distribution, any outcome is equally probable. In other words, this distribution has high entropy.

Classifiablility

Most contemporary image classification models will output a probability distribution over object classes (Human, Dog, Car, etc.) for a given image. Each object is assigned a probability, telling us how likely it is that this object is represented in the image. If an image contains recognizable content, we would expect this probability distribution to have low entropy.
Lets say, for example, we have an image of a car and apply our classification model to it. If our model works, it will assign high probability to the class “car” and low probability to the remaining classes.
Therefore, if we are measuring the quality of a set of generated images, we would want the probability distribution over classes that is provided by some classification model to have low entropy for all images.

Diversity

If a set of generated images is diverse, then most images will depict very different content. Hopefully, all object classes have approximately the same frequency of occurrence in our set of generated images. That means if we average the probability distribution over classes (provided by some classification model) of all the images in our set, the resulting distribution should approximately be uniform.
In other words, this averaged distribution should have high entropy.

Fréchet Inception Distance

One downside of the Inception Score is that the generated images are not compared to real images. The Fréchet Inception Distance was proposed by Heusel et al. in 2017 and addresses this limitation.
Instead of evaluating a set of generated images by itself, it will be compared to a set of real images. However, instead of comparing the images in their RGB representation, we use a representation that was learned by a classification model. These representations contain vision-relevant features.
We assume that these image representations are Gaussian distributed and estimate the mean and covariance for both the set of generated images and the set of real images. The Fréchet distance (Dowson and Landau, 1982) is then computed between these two Gaussian distributions, giving us a measure of image quality for the generated images.

Heusel et al. further demonstrate how the Fréchet Inception Distance is surprisingly consistent with human judgement.

References

Tim Salimans, Ian Goodfellow, Wojciech Zaremba, Vicki Cheung, Alec Radford, and Xi Chen. Improved Techniques for Training GANs. Conference on Neural Information Processing Systems, 2016.

Claude Shannon and Warren Weaver. The Mathematical Theory of Communication, 1949, Univ of Illinois Press. ISBN 0-252-72548-4.

Martin Heusel, Hubert Ramsauer, Thomas Unterthiner, Bernhard Nessler, and Sepp Hochreiter. GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium. Conference on Neural Information Processing Systems, 2017.

D.C Dowson and B.V Landau. The Fréchet Distance Between Multivariate Normal Distributions. Journal of Multivariate Analysis, Volume 12, Issue 3, September 1982, Pages 450-455.